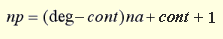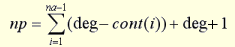Relationships between control points, degree, continuity and number of arcs
The following equations show the relationship of
the number of control points as a function of the degree of the curve, its continuity, and the number of arcs
in a NURBS curve. The equations differ depending on whether continuity is the same at each joint or not.
- When continuity is the same at each joint (which happens in most cases):
| (1) |
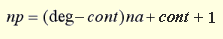 |
where:
| np |
is the number of control points |
| deg |
is the degree of the curve |
| con |
is the continuity of the curve |
| na |
is the number of arcs. |
- When continuity can be different at each joint (as, for example, in the case of a curve obtained by joining a chain of existing curves):
| (1') |
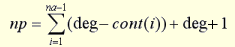 |
where:
| np |
is the number of control points |
| deg |
is the degree of the curve |
| cont(i) |
is the continuity between the i-th arc and the next one |
| na |
is the number of arcs. |
From equations (1) and (1'), you can see that by increasing the degree
of a curve, you can increase its flexibility.
By
increasing the number of arcs, you can obtain "local control." Thus,
if there is more than 1 arc, you can move each of the control points on
the curve without changing the position of the other control points.
If you enter only the minimum number of control points (equal to
the degree of the curve plus 1), you obtain a curve with a single arc
(i.e., a Bezier curve).