Warnings of the Capping command related to incompatibilities
The Capping command performs compatibility checks for tangency, curvature and position continuity among the existing constraints.
When an incompatibility is detected, an appropriate warning is displayed. In such situations, as there is an actual mathematical incompatibility, in order to obtain an acceptable result, it's not possible to indicate a general strategy. Generally, you just have two alternatives:
- Modify the geometry so that the incompatibility conditions are removed from the points where the issues occur
- If possible, apply lighter constraints (for example, if you are applying curvature continuity, apply only tangency continuity, etc.).
See below some typical incompatibility situations.
Compatibility check for tangency continuity
An incompatibility in tangency occurs whenever two curves used as constraints meet at a point where they have different tangent planes.
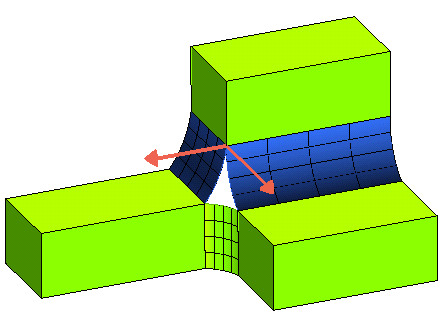
The picture below displays an incompatibility between the blue surfaces. The two red arrows show the normal vectors of the tangent planes at the common point. As you can see they are not collinear.
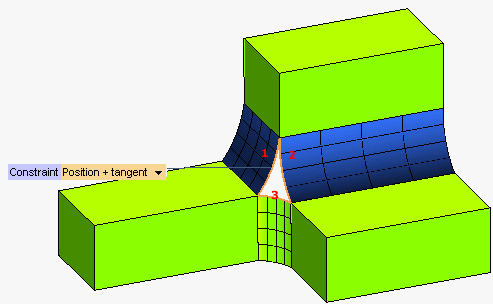
If you start the Capping command, select the three curves as in the following picture and set the Constraint to Position + tangent:
after asking for a preview ( 
) the Show Warnings button ( 
) is displayed. If you click it, the following warning will be displayed:
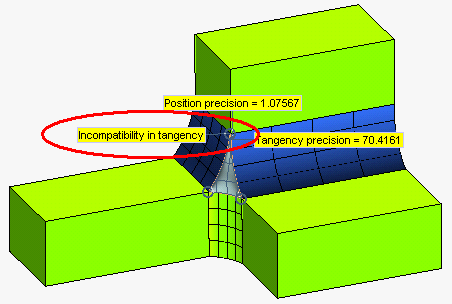
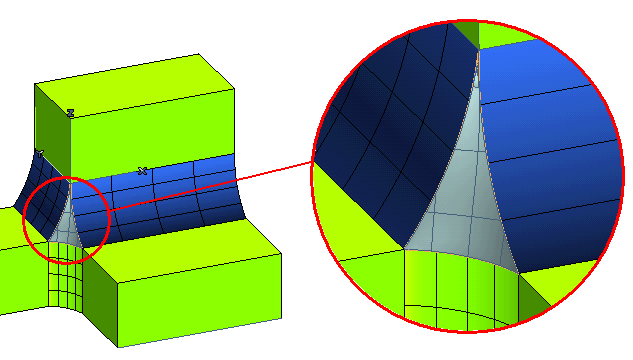
When such a warning is displayed, to obtain an acceptable result beyond the mathematical incompatibility you can modify the involved geometry in order to remove the critical situations or apply lighter constraints. For example, if you apply only Position continuity to the above model, you will get a clean result with no warnings.
Compatibility check for curvature continuity
An incompatibility in curvature occurs at the point where two curves having different curvatures meet.
In the following picture, there are two points of incompatibility in curvature (in yellow). It's easy to see that the curvatures of the cylinders are not the same, even if there is no incompatibility in tangency at these points, since there is a common tangent plane.
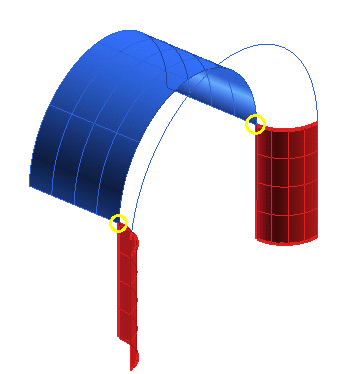
If you start the Capping command, select the three curves as in the following picture as Group 1 setting the Constraint to Position + tangent + curvature, and the fourth curve as Group 2 with the Constraint set to Position:
after asking for a preview ( ) the Show Warnings button ( ) is displayed. If you click it, the following warning will be displayed:
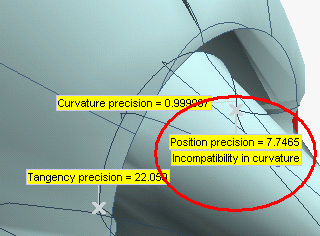
When such a warning is displayed, to obtain an acceptable result beyond the mathematical incompatibility you can modify the involved geometry in order to remove the critical situations or apply lighter constraints.
Compatibility check for position continuity
An incompatibility in position occurs when two different points of two constraints have a common projection point onto the initial shape.
Here are some typical situations in which an incompatibility in position occurs.
In the case of a grid of curves, like in the following example, suppose the blue curves are selected as Constraint Boundaries and the brown curves are selected as Constraint Internal Curves.
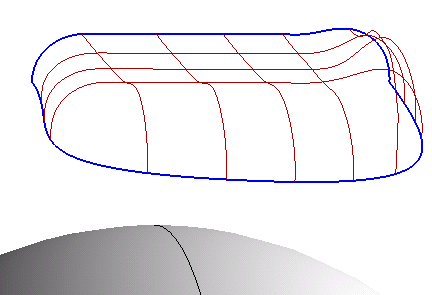
What you get after asking for a preview ( ) and clicking the Show Warnings button ( ) is the following warning:
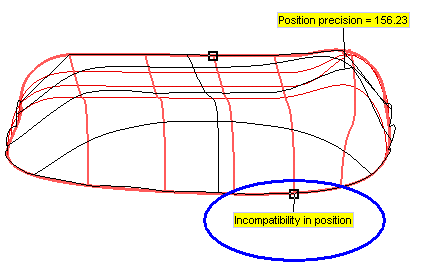
As you can see in the picture below, even if the initial curves do not intersect, their projections on the initial shape do, and this generates the incompatibility situation.
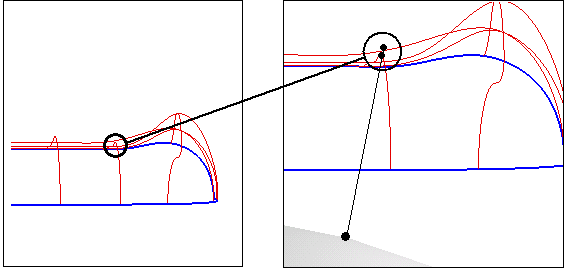
Another critical situation is when there is incompatibility between boundary and internal curves, like in the following model.
The black curve does not intersect the green one, but their projections on the initial shape coincide.
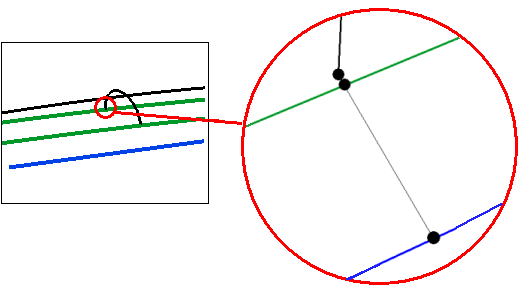
So, if you select the green curves as boundaries and the black one as internal constraints, indicate an initial single curvature shape using the blue line as the axis, you will get the following warning:
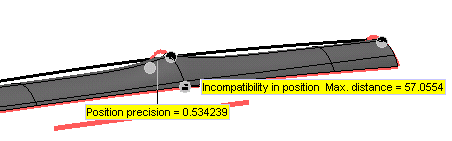
Finally, there are situations in which an incompatibility in position can occur only when just one curve is involved. If there is a silhouette in the direction of projection, different points may have the same projection onto the initial shape.
In the model of the following example, suppose you select the blue curve as a boundary constraint and the brown one as an internal constraint.
The warning you will get is the following:
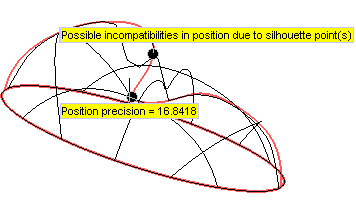
In fact, the two black points in the picture below are the silhouette points of the curve in the direction of projection.
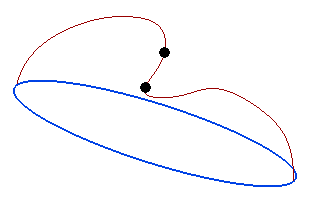
In the neighborhood of the silhouette points, you can find a lot of couples of points having the same projection onto the initial surface (in the example, the three red points have the same projection).
