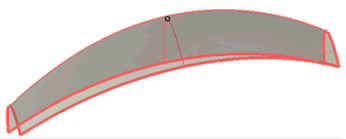
the two curves on top seem to intersect, though they don't actually do:
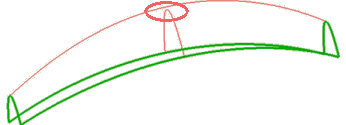
and the surfaces you would get with the ordinary Capping methods would have a kind of "bump" in the area of the virtual intersection:

In order to improve the shape of the resulting surface of the Capping command, in certain cases of incompatibility, it is possible to create a capping surface by using virtual vertices: a virtual vertex is defined when two curves are supposed to "cross" each other without necessarily having real intersections. The said situation refers to positional incompatibilities, but virtual vertices can be used to solve tangency or curvature incompatibilities as well.
| Note Please note that virtual vertices are by no means a method to solve or even to bypass chaining issues along the boundaries: boundary curves always need to be correctly chained. The situations in which they can be profitably applied are described below. |
When the intersection among the selected curves (for example between a boundary curve and an internal curve) is not real, the surface you would get might not be as good as expected or required.
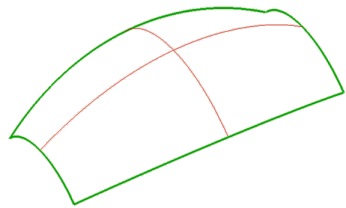
For example, in the following model ("capvv.e3" in the samples folder):

the two curves on top seem to intersect, though they don't actually do:

and the surfaces you would get with the ordinary Capping methods would have a kind of "bump" in the area of the virtual intersection:

In such a case, in order to improve the surface quality, you can proceed as follows.
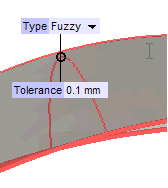
| Free | No constraint is applied. The resulting surface is not constrained to be really "through" the selected curves. |
| Fuzzy | If this option is selected, when the two curves do not really intersect, the constraint is not applied to a specific point, but just somewhere within the tolerance. So the resulting surface will be "through" some point on the curves, in a distance within the tolerance. |
| Strong | If this option is selected, when the two curves do not really intersect and the tolerance is big enough, in addition to the Fuzzy behavior, there will neither be any gap between the resulting surface and the curves, nor any planar zone around the vertex. |
As you can see, the final result is much better: