You have a non-manifold solid for whatever reason. Regardless of what caused this situation, in many cases you can ignore this problem and go ahead using the solid as is. In fact, non-manifold solids can even be used as a powerful feature of the think3 application.
What you need to know:
Non-manifold solids are a representation of solids that are not "real solids" as real workpieces. They may at times be a result of a incorrect modeling step, or an unexpected result in turning legacy surfaces into a solid.
When you can usually ignore this problem and proceed:
Typically open solids are used to cut other solids, or between them, as a pure trimming tool. Here is a typical example of how an open solid can cut a true solid:
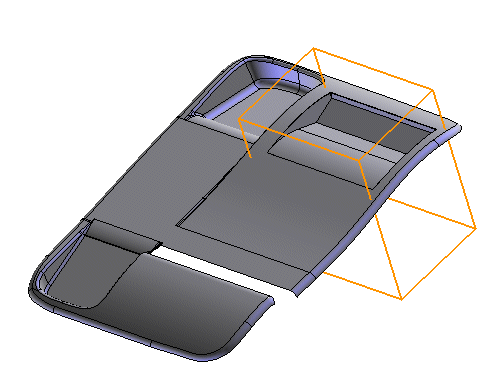
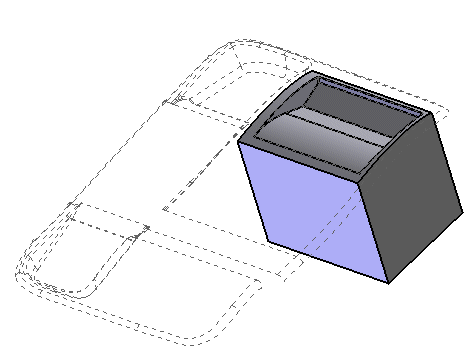
All these of cuts are done using the command Insert-Solid-Boolean. The possible results are always four (A+B, A-B, B-A, AintersectsB), but, working with open-solids it's sometimes difficult to predict what final result you'll get. The theory is the following:


If the normals of the open solid are pointing "up", it means that the open solid can be considered as one with infinite thickness in the opposite direction. Given that, the boolean operation that was used in the previous example is an "intersection" between the open solid and the cube.
Notice that two open solids, or an open solid and a true, manifold solid, can be combined using a boolean ONLY if the open solid has the "right" topology in the area that intersects.
An example might help:
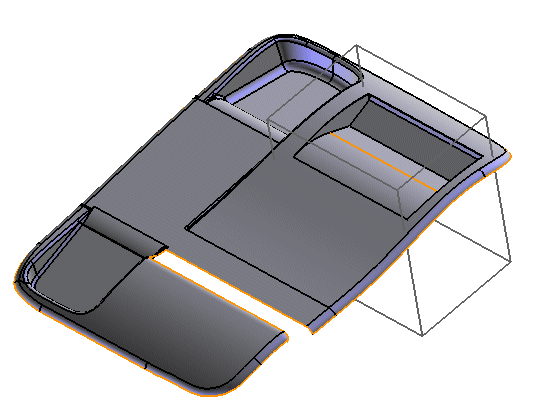
The open solid (modified from the previous one) has incorrect topology. See the highlighted "strip." Now, if the strip does not touch the intersecting area, you'll get a new open solid with the same fault.

But, if the strip of the open solid "touches" the intersection area (notice that the cube has been reduced along the X axis so that it will intersect the strip of the open solid).
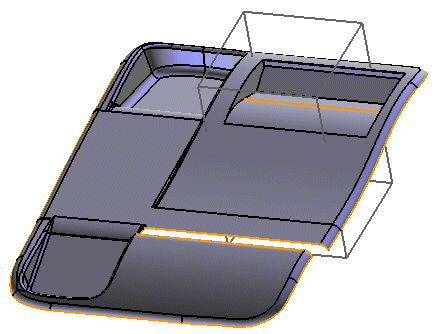
The resulting object will be an unusable non-manifold solid.
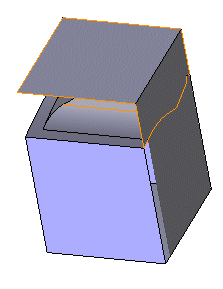
Given that, let's analyze what happens working with two open solids. Actually it becomes difficult to predict what kind of object you'll get making a boolean operation between them. See example below:

Two open solids, the grey one and the brown one. Note that the two solids are really "open."

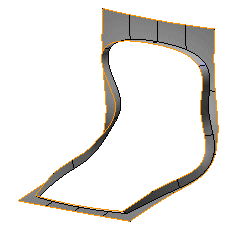
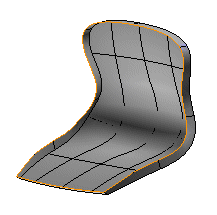
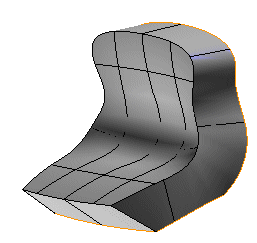
So, combining the two open solids, you could get these four resulting shapes (notice also that the result can also be an open solid).
Again, since it's difficult to predict which result you will get,a tool is available that will help you determining which boolean you need. Download it from think3 download
area.
There are two main cases:
- applying features to an open solid
- applying features to a "generic" non-manifold solid.
Applying features to an open solid
This will follow the same scenario of Booleans with open solids (above). In other words, you can't apply features (such as fillets, hole, pins) on an open solid if the feature will "touch" an existing strip. See example below:
On the above solid ...
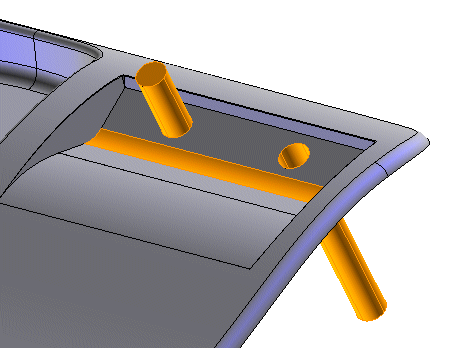
we added a pin, a hole, then a fillet ...
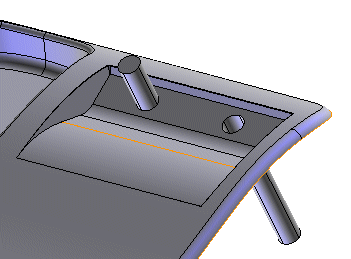
but since the solid has a strip on it:
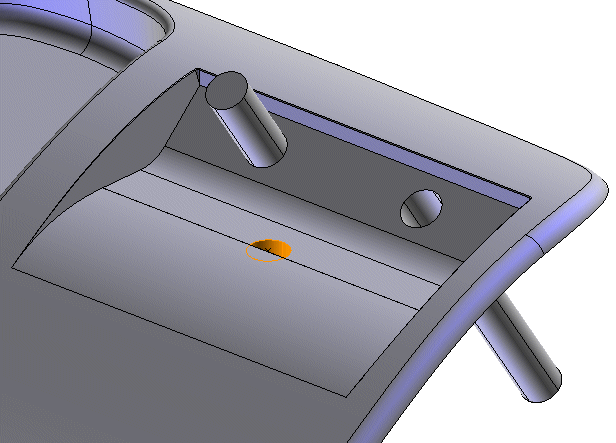
we can't add any features that are crossing that strip (or, you can, but the resulting object will have problems down the road).
If you need to add a features on that strip, you have to fix it before applying the feature. Search the Knowledgebase for real world cases.
Applying features to a "generic" non-manifold solid
A generic "non-manifold" solid is a solid where you got the warning "non-manifold" object, but you can't easily determine what kind of problem it might have. Usually, it's a problem of vertexes, sometimes it might be a problem of overlapped or partially overlapped surfaces. See non-manifold solids.
If you don't take the time to check and fix the issues described above, and decide to continue using features, everything may work, until you apply a feature on an overlapped face or on incorrect vertex. The feature will fail or it won't be even possible to apply in it that area.
Actually a "generic" non-manifold object or even a open solid can be used to get a 2d drawing. See examples:
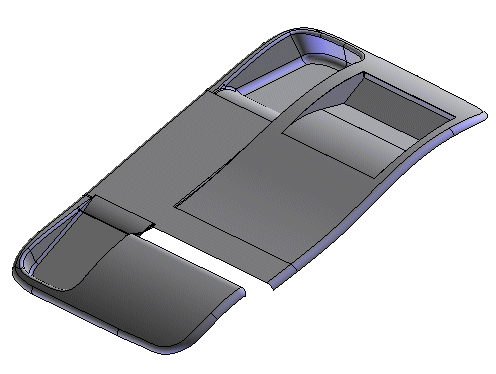
You can get a 2D drawing of an open solid. actually you can also make 2D sections but, obviously, the section won't have a thickness.
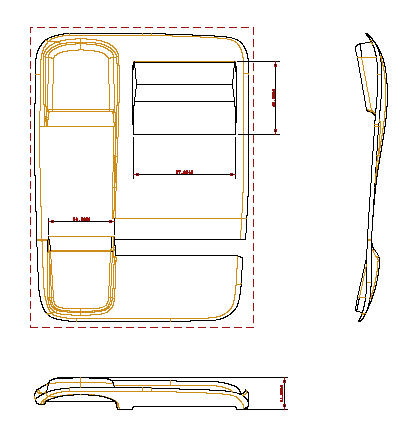
Or, working in a "almost closed" model (see the strip on the top)...

It will be possible to get a valid 2D section + capping, if the section won't touch the open edge (the strip).
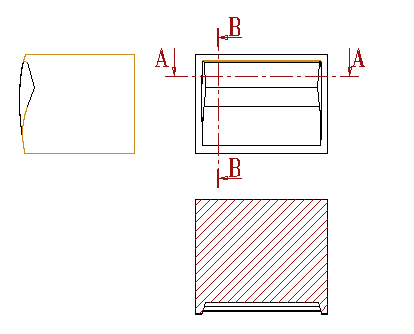
See for instance sect BB. It gives an empty section. Note that the program just warns you if you try to get a section from a non-manifold object. It doesn't mean that you can't!