What is the curvature of a surface?

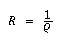
At each point P on a surface s, the curve G of intersection between s and any plane p containing the normal n to the surface at P has a defined curvature r and a radius of curvature defined by the equation:

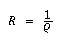
There are many planes that can contain the normal n. The mathematician Euler showed, however, that there is only one direction in which the radius of curvature has an absolute maximum and only one direction in which it has an absolute minimum. The curvatures in these directions are called the principal curvatures.

If Q is the angle made by a plane p passing through the normal n and the plane p₂ corresponding to the maximum principal curvature, and if R₂ is the maximum radius of curvature and R₁ the minimum radius of curvature, then the radius of curvature R in the direction of the plane p can be found with Euler's formula:

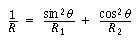
Two combinations of the principal curvatures are of particular interest — the half sum of the two principal curvatures and their product.
 

• The mean curvature:
  
  
   
• The Gaussian curvature(or total curvature):

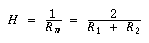
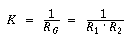
The mean curvature is particularly important since, of all the surfaces delimited by the same closed curve, those whose mean curvature is zero (Rm = 0) are the surfaces with the smallest area.

Instead, the Gaussian curvature at a point P is such that:
 

• When K < 0
  the maximum curvature and the minimum curvature have opposite signs; in the proximity of P, the surface crosses the tangent plane and takes on the shape of a saddle (for example, hyperboloid of one sheet).
• When K = 0
  one of the two curvatures is zero, so that the curvature always has the same sign as the other principal curvature; therefore, in the proximity of P, the surface lies all on the same side of the tangent plane (for example, cone or cylinder).
• When K > 0
  the maximum curvature and minimum curvatures have the same sign: again, in the proximity of P, the surface lies all on the same side of the tangent plane (for example, ellipsoid).

Given a surface s, consider a normal plane section through a certain point P (see the green plane in the following illustration and the red curve). Then consider the blue plane containing the direction v on the surface. The blue curve is the intersection of the blue plane defined by vector t and direction v in the tangent plane. Let its radius of curvature be R'. The red curve is the intersection of the surface with the normal plane defined by the normal n and the direction v. Let its radius of curvature be R.

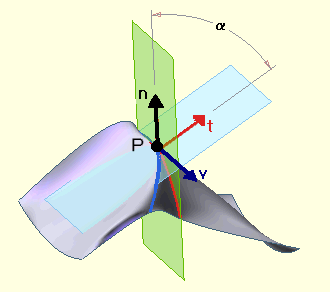
If a is the angle between the two planes, then Meusnier's theorem asserts:

R'=R cos a