Texture Space and Texture coordinates

Textures in think3 applications comprise of images. Texture mapping applies a pattern of color to an object. A texture, generally speaking, is a function describing an object property as a variable. For example, the color of an object is typically defined as a triplet {R, G, B} value as:

In a similar line of thought, for textures, the function can have 1, 2 or 3 variables, defined on domains of variation, called the Texture Space. Texture space is measured with the coordinates u, v, and w. u represents horizontal (left to right), v represents vertical (top and bottom), and w represents depth (for 3D textures). These coordinates are known as the Texture coordinates.

In think3 applications, we use only the u and v coordinates, describing a 2D texture space. So the variable w is not required. If you look at a texture map, the origin (u=0,v=0) is always the lower left corner. The upper left is (0,1) - lower right is (1,0) - and upper right is (1,1). This holds true regardless of the size or shape of the texture. So the textures, like bitmaps, can be represented as a two-dimensional array of color values. The individual color values are called a texture element, or texel. Each texel has a unique address in the texture. The address can be thought of as a column and row number, which are labeled u and v respectively. Texture coordinates are in texture space. That is, they are relative to the location (0,0) in the texture. The following image illustrates this:



When a texture is applied to an object in 3D space (for example, a sphere) we need to assign the object, the texture coordinates. In short, the process of mapping the texel addresses to the object coordinates, is the actual Texture mapping. The following image illustrates the texels in the above texture map. In this, the middle texel will have a texture coordinate of (0.5, 0.5).

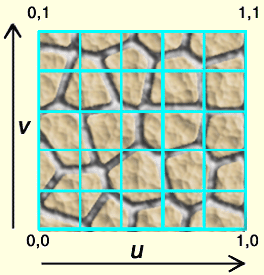
There should not be any confusion between geometry coordinates and texture coordinates.The geometry coordinates exist for the (3D) objects, to which we do the Texture Mapping. The difference between texture coordinates and geometry coordinates are what they measure. The geometry coordinates (x, y, and z) are a reference system for placing geometry in a three dimensional space. An object exists at one set of coordinates. If you move the object, it gets at a new set of x, y and Z values. The same happens when you scale or rotate an object.

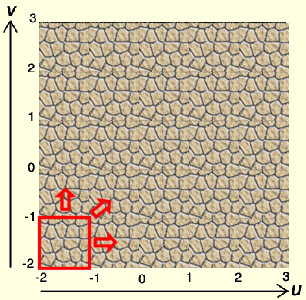
The texture coordinates only measure texture repetitions. That's why the upper right corner is (1,1). It will always be (1,1) no matter how you scale or stretch the texture. The space between 0,0 and 1,1 is one repetition of the texture. If you use more than one repetition, you start tiling the texture. Each tile adds 1 to the u and/or the v coordinates (or subtracts 1 if you want to tile it in a negative direction). So a set of texture coordinates from (-2,-2) to (3,3) would be a grid of five tiles of our texture, as shown below:

Mapping Surface and the S,T coordinate values

Texture space is a mathematically perfect, flat surface. That is, it does not have any curvature. However, the surfaces that textures are going to be placed on (surfaces of objects) are seldom going to be flat. That is, texture mapping should consider the mapping of a flat surface (the texture map) onto a curved one. This surface to which the texture space is to be projected, is called a Mapping Surface. So we need yet another coordinate system to define Mapping Surface.

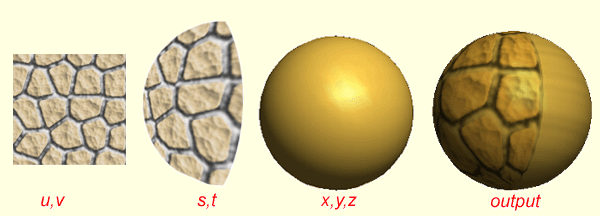
Mapping Surface is defined with the coordinates s and t, with s being the horizontal component and t being the vertical. (s, t) coordinates are functionally equivalent to u, v coordinates but they represent a totally different concept. Since the surface being mapped would be irregular, s, t coordinates let us find a particular spot on the texture map (u, v coordinates) regardless of any stretching or distortion that might have taken place in order to get the 2D texture onto the 3D surface. In other words, the u, v coordinates of the 2D image are referenced by the s, t coordinates on the surface that relate to the x, y, and z coordinates of the 3D object's geometry. So the actual texture coordinates are represented by the (s,t) coordinates. The following image illustrates this transition from the (u,v) coordinates of the texture map to the (x,y,z) coordinates of the object through the (s,t) coordinates of the mapping surface.



Note
It should be clear that the (s,t) coordinates are the actual texture coordinates. Only in the case of UV mapping the (u,v) coordinates are equivalent to (s,t) coordinates. This is due to the fact that a plain surface (texture map) is being mapped to another (of the object) surface by considering that the surface is planar.