Continuity Types
Continuity is the mathematical way to indicate how smooth the flow between two curves or surfaces is.
The main types of continuity are two:
- G continuity (geometric continuity)
To fulfill G0 continuity, two curves must join together at an endpoint. To fulfill G1 continuity, (using the first derivative) the directions (and only the directions) of the tangent vectors of the two curves at the joint must coincide. GN continuity implies that the N'th derivatives of the two vectors be equal in direction.
- C continuity
To have C1 continuity the two tangent vectors must be equal in both magnitude and direction. So, CN continuity implies that the N'th derivatives of the two vectors be equal both in magnitude and direction.
Here is a brief description of the main G continuity levels available in think3 applications.
- G0 or Positional continuity.
Two curves having a common endpoint, with no further condition, are positionally continuous. This is the less smooth type of joint, as the only condition to satisfy is the common endpoint, no matter what the flow of the two curves around the joint may be.
- G1 or Tangency continuity.
Two curves having a common point and tangent vectors lying along the same direction are said to have tangency continuity. The two curves may seem to have the same direction at the joint, but the way they change their direction may still be very different (the rate of this change of direction is called curvature).
- G2 or Curvature continuity.
Two curves having a common point, tangent vectors lying along the same direction, and having the same curvature (which is, the same rate of change of the direction) are said to have curvature continuity. The directions at the joint seem to change with the same "speed".
- G3 or Torsion continuity.
Two curves satisfying the same conditions as the ones having curvature continuity, and, in addition, having the same constant rate of change of the curvature are said to have G3 or torsion continuity.
- Smooth curvature continuity.
Two curves having G3 continuity are said to have Smooth curvature continuity at a joint if there is tangency continuity between the two curvature plots.
- G4 or Curvature plot curvature continuity.
Two curves having G3 continuity are said to have G4 continuity at a joint if they have the same rate of change of the rate of change of the curvature, which is the same rate of change of torsion. In this case there is curvature continuity between the two curvature plots.
(*) The osculating plane W of a curve at one of its points is the plane formed by the principal normal (n) and the tangent to the curve at that point (t).
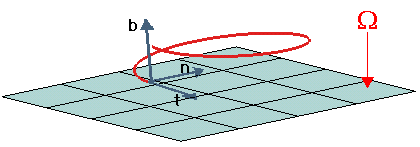
(**) Torsion is the rate of change of the osculating plane along a curve and is a measure of the deviation of a curve from a plane.

