How to Define an Axis or a Line

Several different methods are available to define a line, an axis or a direction:

Line To define the direction as the one of an existing line to be selected just by clicking on it.
A Set direction/axes using X, Y, Zcheck box is available in the Input category of the System Options so as to enable you to choose how to define direction/lines as parallel to one of the axes of the Work Plane.
  • When the check box is not selected you can define the direction as parallel to one of the axes of the Work Plane just by choosing the Line option and by clicking on one of them as displayed in the image below.



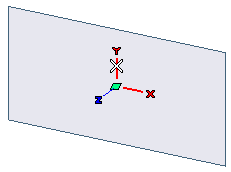
    In this case by default the actual line will be the one through the origin of the system. However, you can change the origin by resetting the Origin selector and by specifying another point the line must be through, though retaining its direction.
    In this case the drop-down list will not include the X,Y,Z choices. Yet, once a Work Plane direction has been selected, the corresponding letter (X),(Y),(Z) will be displayed adjacent to Line.
  • When the check box is selected you will still be able to use the interactive direction described above, but the direction/axis definition drop-down list will include:
    Parallel to X and through point To define the direction as parallel to the X axis of the Work Plane and through a point to be specified.
    Parallel to Y and through point To define the direction as parallel to the Y axis of the Work Plane and through a point to be specified.
    Parallel to Z and through point To define the direction as parallel to the Z axis of the Work Plane and through a point to be specified.
2 points To define the direction as the one identified by two points to be selected.

When appropriate, all or some of the following options will also be available.

Tangent to curve To define the direction as the one of the tangent to the selected curve in the point used to select it (*).
Normal to curve To define the direction as the one of the normal to the selected curve in the point used to select it (*).
Binormal to curve To define the direction as the one of the binormal to the selected curve in the point used to select it (*).
Normal to surface To define the direction as the one of the normal to the selected surface in the point used to select it.
First tangent to surface To define the direction as the one of the first tangent (U parametric direction) to the selected surface in the point used to select it.
Second tangent to surface To define the direction as the one of the second tangent (V parametric direction) to the selected surface in the point used to select it.

(*) Let g=g(u) be a 3D curve. The trihedron known as Frenet frame (or reference) is the one identified by (t(u), n(u), b(u)) where:
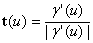        is the unit tangent
        is the unit normal
  is the unit binormal.

These definitions do not depend on the specific parameterization. The three vectors identify three planes at each point of the curve: